Time value of money- an intro
Tvm is a core financial concept of which (ordinary) people are aware of.
And that is the reason why all people want to perceive money now and pay money later
But why is so?
Because the same sum of your money is worth more now than later!
Consequently, the sum of money in your hand has greater value than the same sum to be paid in the future.
This is a concept of TVM!
So, formulas for computing the time value of money include nowadays amount of money-Pv, its future value-Fv, the interest rate, and of cause the time frame.
Could you with no vague understanding, provide a clear answer to next 2 (simple) questions:
Let’s say that one decided to have 1M by age 60?
Or
When you get a mortgage loan you are usually given the option to buy down the loan interest rate by paying points up front
Take advantage or reject the above option?
The economic decision is followed: is worth paying some cases now to have lower interest in the future-this is TVM question
If you couldn’t, then you have to pay attention to posts accompanied by this page
Reasons for such are few!
Fully understanding given answers is just an initial step toward a clear understanding next important term: time value of bankroll, TVB
Of cause,o if you want to benefit from this portal on your own that is free of charge
Au contraire if not, in order to benefit you will need to subscribe to specific posts on that topic
About the nature of interest rate
The interest rate can be twofold in its nature: simple or compounded
Simple interest is based on the original principal amount of a loan or deposit e.g., buying a car through n equal payments + appropriate interest (say 2% to the whole price of the car)
Simple interest
Interests on year basis
If we denote invested capital, Principal, as C,
The interest rate for one year as i/100 (e.g. 4/100)
Then after one year, a given amount of money I=I(C,i):
I=C*i/100
After n years:
I(n)=n*C*i/100
Example:
The principal in the amount of 3000€ was invested as savings for a period of 2 years with a fixed interest rate of 4%
How much do you get (simple)interest on savings for those 2 years?
Example:
The principal in the amount of 3000€ was invested as savings for a period of 2 years with a fixed interest rate of 4%
How much do you get (simple)interest on savings for those 2 years?
I=nCi/100
I=230004/100=2304=240€
Suppose we take a dedicated loan from a bank to buy a car under the same, above conditions
As it is a simple interest rate every year we need to pay down (3000+240)/2=1500+120=1620€ per year, over a period of 2 years
I=nCi/100
I=230004/100=2304=240€
Suppose we take a dedicated loan from a bank to buy a car under the same, above conditions
As it is a simple interest rate every year we need to pay down (3000+240)/2=1500+120=1620€ per year, over a period of 2 years
Interests on monthly basis
One year has 12 months, so if I(x) denote interests based on x months, first we must start from the ratio:
I(x):I(1 year)=x:12
From that ratio we ‘jump in’ on the final formula:
I(x)=I(1)x/10 I(x)=xCi/12100
I(x)=x*C*i/1200Example:
The principal in the amount of 3000€ was invested as savings for a period of 20 months with a fixed interest rate of 4%
C=3000€
i=4
x=20
I(20)=2030004/1200=30004/60=504=200€
Interest in a Per-Diem Basis
Consensually one year has 365 days so as in the previous deduction we find:
I(x):I(1)=x:365 x=number of days
I(x)=x*C*i/36500Example:
The principal in the amount of 3000€ was invested as savings for a period:
from 3. February 2020
to 18 august 2022
with a fixed interest rate of 4%
First, we have to find the actual number of days in a given interval
Let ms excel do it for us:
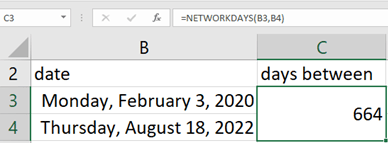
if given values plug into the formula:
I(x)=xCi/36500
thus we get:
I(664-1)=66330004/36500 =217.9726 €
Compound interest
They are based on the principal amount and the interest that accumulates on it in every period: interest in the second period is generated from stake + interest rate from that previous period
In finance, Compound interest is based on the principal amount and the interest that accumulates on it in every period.
“In real-life situations, compound interest is often a factor in business transactions, investments, and financial products intended to extend for multiple periods or years. Simple interest is mainly used for easy calculations: those generally for a single period or less than a year. Simple interest also applies to open-ended situations, such as credit card balances.”
Investopedia
Heuristic example:
Suppose that the bank for our 1-year savings provides a 12% interest rate
Remember: on client-side the interest rate is given on yearly basis!
Here it means that the bank gives a monthly 12/12=1% interest rate
If we deposited 100€ in our savings account at the beginning of 2. months we earned 1001/100=1€ Now our principal is worth 100+1=101€ =100(1+1/100)
At the beginning of 2. month our savings is: 101 + (101)1/100=101(1+1/100)=100(1+1/100)2
At the beginning of 3. months our principal C is 100(1+1/100)2 and all increased by the interest factor (1+1/100) so we get those states for principal at the beginning 3. months:
100(1+1/100)2 +100(1+1/100)2 1/100=100(1+1/100)2(1+1/100)=100(1+1/100)3
………
………
At the end of the current year, we earned: 100*(1+0.01)12
The general formula for compounding by a yearly basis:
Fv(n)=Pv(1+p/100)n (i The general formula for compounding for n years but on by monthly basis:
Fv(n)=Pv(1+p/1200)n*12If compounding occurs m times per year:
Fv(n)=Pv(1+p/(m*100))n*m (ii Effective annual rate
Why EAR?
Briefly, it is a tool for comparing different cash flows from different origins and purpose
The effective annual rate also called annual equivalent rate (aer) equates formula (ii with (i :
Pv(1+p/(m*100))n*m = Pv(1+ aer)n => aer= (1+p/(m*100)m -1
Effective annual rate:
aer=(1+ r/m)m -1
The most important feature of the are:
- takes into account the fact that more frequent compounding periods will lead to a higher effective interest rate(border case is so-called continuous compounding)
- is important because, without it, borrowers might underestimate the true cost of a loan.
- investors need it in order to project the actual expected return on an investment
Continuous compounding
What happens when m goes to infinity?
Simply- continuous compounding
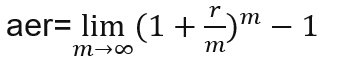
Suppose that unit for compound frequency is 1 second!
So every second the interest is entered
One minute has 60 sec
One hour has 60 minutes
One day has 24 hours
One Year has 365 days
So in 1 year, 60*60*24*365= 31 536 000 transactions are accomplished
How much is aer(r) for such a value of m?
Finite or almost infinite?
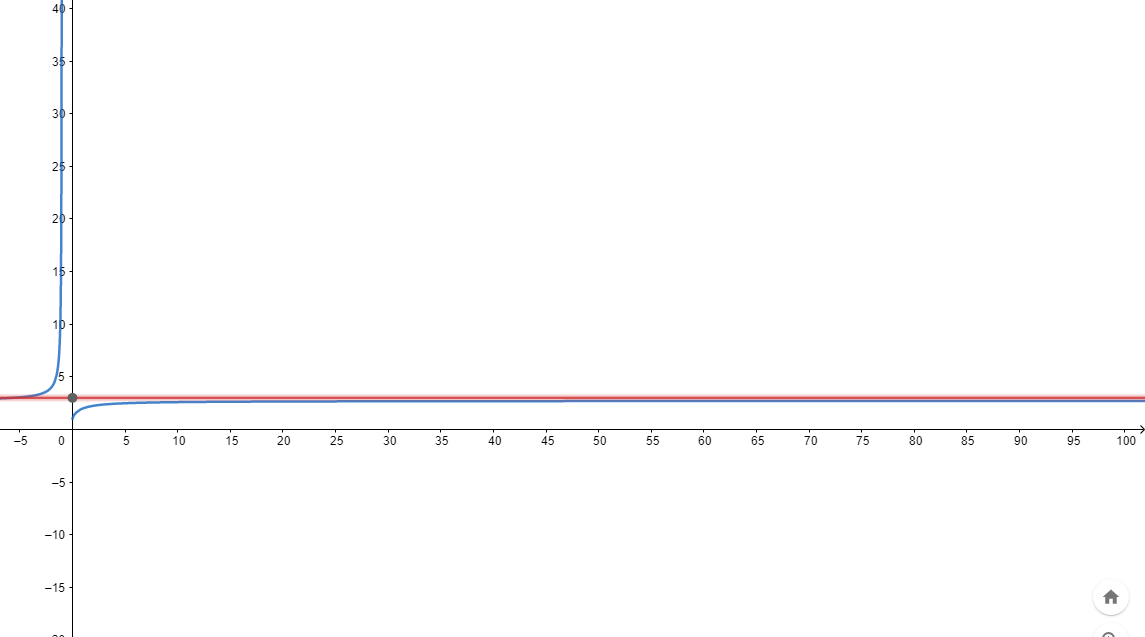
For this purpose’s sake, let’s take under consideration the next function:
y(x)=(1 + 1/x)x
in half-plane x>0
from the picture, we can premature conclude that always is y<3(red line)
Excel can help a little bit, just to encourage us that we are on a good way:
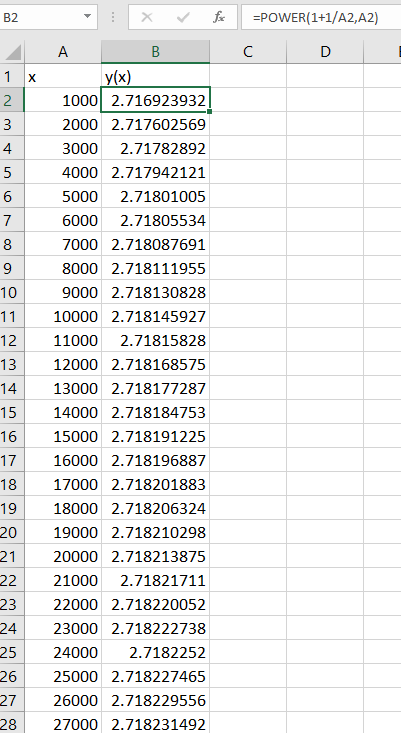
Yet to be sure, let us calculate in a couple of steps Lim y(x) when x goes to + infinity by the L’Hospital rule
step1 logarithm:
Ln(y(x))=x*Ln(1 + 1/x)
step 2-transforming:
Ln(y(x))=Ln(1 + 1/x)/(1/x)
step 3: derivative right side + l’Hospital +derivative right side + l’Hospital:
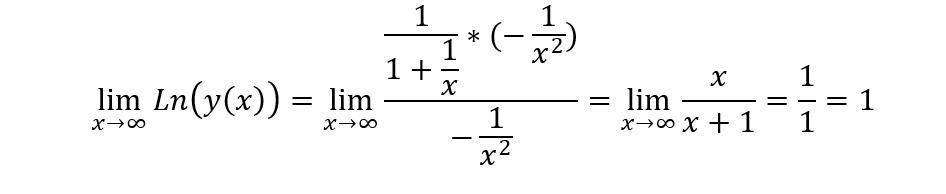
So
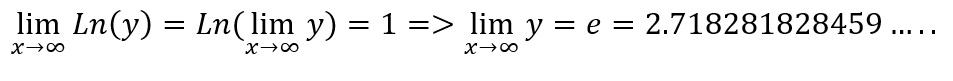
In the same manner, could be a calculated expression
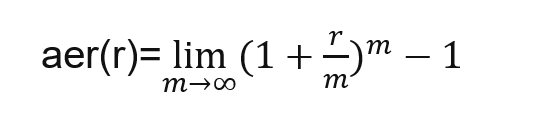
but for creativity’s sake let’s do something else
substitution: r/m=1/u =>m=r*u
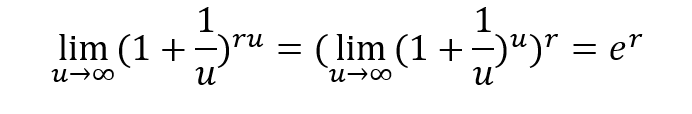
So even frequent compounding periods will lead to a higher effective interest rate there is the so-called Supremum (the greatest upper frontier): er