Arbitrage betting

According to one definition Arbitrage betting or simply Arb is:

”  a betting style where all possible outcomes of a single game are covered.
ARB betting options are rare and arise when sportsbooks have varying opinions on the proper odds for a match.”

As many people as their definitions, so we have another one with words of caution:

” When you back all possible outcomes on an event, backing odds from different bookmakers to mathematically g

guarantee a profit.
Bear in mind that it comes with significant risks.”

And so on and so forth

Let’s come to the point!

Mathematical foundations of Arbitrage betting

These foundations must provide practical answers to the following questions:

• how this method differs from the Dutch book compiled by the bookmaker
• when its effects occur
• what is the profit of the punter, or what is the loss of the bookmaker

The main theorem of Arbitrage  betting: Arbet theorem

Let d.o'(1), d.o'(0), and d.o'(2) be the odds values by which is Dutch book formed
(e.g.
Liverpool- Wolverhampton Wanderers
1 0 2
1.35 6.50 12 )

Conclusion:

If the harmonic mean of these odds is greater than 3 then the bookmaker is at a loss

Proof:

According to the previous theorem, Arb could take place if and only if it is satisfied:

p’(1)+p’(0)+p’(2)<1

That implies:

d,o’(1)* d,o’(0) + d,o’(1)* d,o’(2)+ d,o’(0)* d,o’(2)< d,o’(1)* d,o’(0)*d.o’(2)

By definition of Harmonic mean, immediately follows:
H(d.o'(1), d.o'(0), d.o'(2))=3* d.o’(1)* d.o’(0)d.o’(2)/( d.o’(1) d.o’(0) + d.o’(1)* d.o’(2)+ d.o’(0)* d.o’(2) )
From the above facts we conclude that is, under the given circumstances, really:
H(d.o'(1), d.o'(0), d.o'(2))>3

Because d.o’(z)=(1-y)d.o(z) z=1,0,2
it follows:
(1-y)2[ d.o(1) d.o(0) + d.o(1)* d.o(2)+ d.o(0)* d.o(2)]<(1-y)3 d.o(1)* d.o(0)d.o(2) since it’s valid: d.o(1) d.o(0) + d.o(1)* d.o(2)+ d.o(0)* d.o(2)= d.o(1)* d.o(0)*d.o(2)
it must be fulfilled: y<0

Q.E.D

Punter’s profit from Arbitrary betting

Let’s find punter profit from negative overround’s accrual:

p(1)+p(0)+p(2)=1- orr

1-orr=1/(1-y) => -y=orr/(1-orr)

So -y is de facto punter’s arb profit!

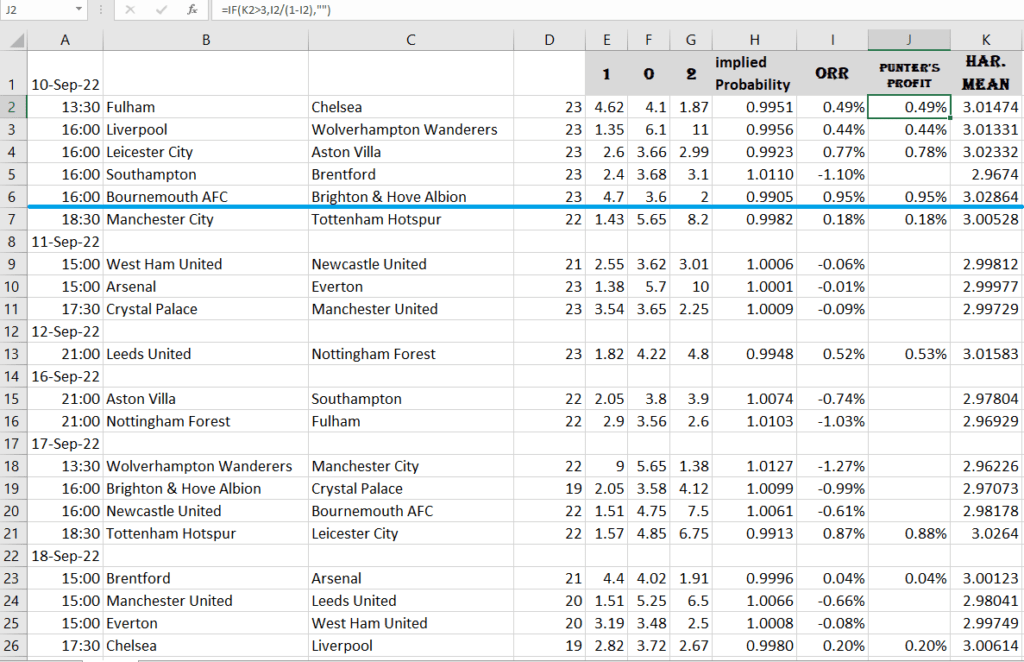
Tracking opportunities for Arbitrage betting

There is a tiny chance that one bookmaker do an error in forming odds which opens a gate for arabing
But if we search for odds at various bookmakers then exists a chance to perform arb
In doing so, this one must be followed next schema:
for all offered coefficients for 1, for 0 for 2, always choose the highest one as is presented in the Odds Math portal

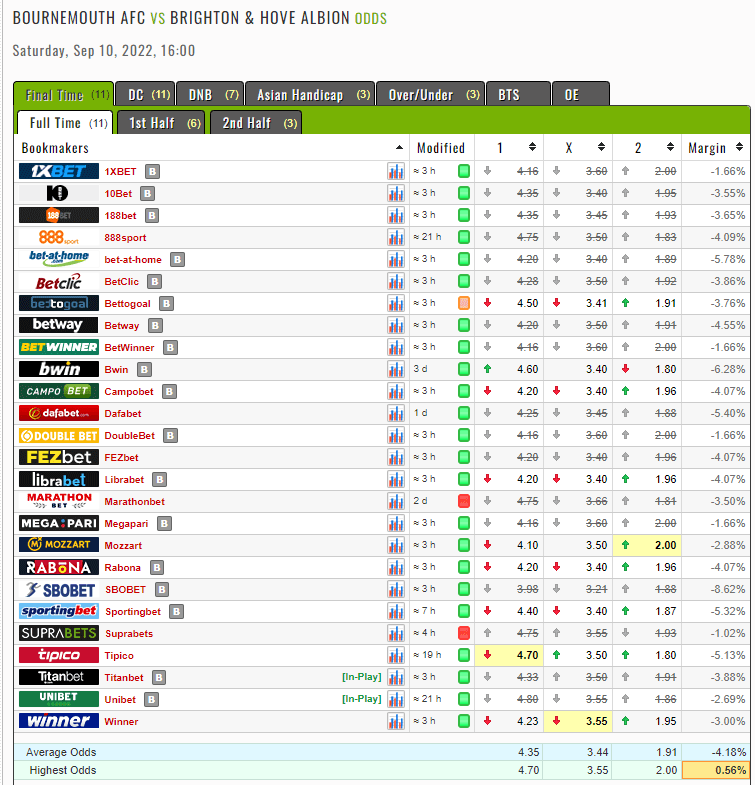
Let’s quantify in this example the apparent opportunity given by  Arb

Highest:
d.o(1)=4.7
d.o(0)=3.55
d.o(2)=2

p(1)+p(0)+p(2)=0.9905 or 99.05%
1-0.9905=0.0095 or 0.95% AND THAT IS VALUE OF OVERRAUND

Punter’s profit comes out by formula: orr/(1-orr)=0.009591

Punter’s profit:0.9591% less than 1% of initial wager!!

Regardless of the previous, here immediately arises the question of the distribution of initial stake throughout the market!
How to quantify sub-stakes?

Distribution of the main Stake in Arbitrage betting

The correct answer to this (practical) question is important not only for this topic but in general!
Because it opens the way to new methods by a complexity far above Arb

Conditions preceding the solution:

• win situation is independent of the outcome (of the event)
• punter’s profit doesn’t depend on the outcome of the event

Notation:

S-initial stake

s(1)-sub stake for a home win

s(0)-sub stake for a draw

s(2)-sub stake for away win

n_profit -punter’s revenue

The above conditions pave the way for the formation of the system of Equations:

s(1) + s(0) + s(2)=S

s(1)*d.o(1) +s(0)*0 + s(1)*0 – n_revenu=0
s(1)*0 +s(0)*d.o(0) + s(1)*0 – n_revenue=0

s(1)*0 +s(0)*0 + s(1)*d.o(2) – n_revenue=0

Arbitrage betting matrix system, FAB-M

The above system can be given a suitable matrix form convenient for working in MS Excel

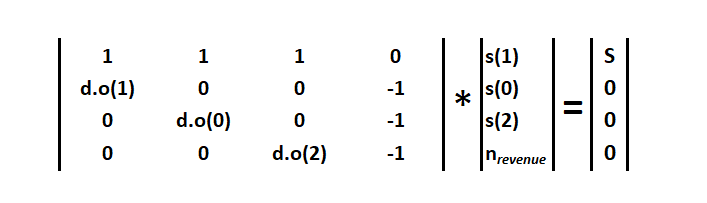
4×4 matrix is Arb matrix
The first 1×4 matrix is the stakes-profit vector
On the right side is the wager vector in the form 1×4 matrix

FAB-M ground theorem

I) let S denote the initial stake

ii) s(1),s(0),s(2) are figures greater than zero

iii) s(1)+s(0)+s(2)=S

All members of the stakes-profit vector are greater than zero including
n_revenue-(s(1)+s(0)+s(2)) if and only if the Harmonic mean of the market is greater than 3

proof:

because i) and ii) all members od profit-vector are greater than zero if n_profit-S>0

According to the main theorem, n_{revenue- S} >0 if H(market) is not lesser than 3

n_profit=0 if probabilities, derived from the market, add up to unity

But in that case p(1)+p(0)+p(2) belongs to the main facet

so, case n_profit=0 is possible only in absence of a Dutch book