Money pump

Money pump and Dutch book

The money pump term,m.p is close to the term Dutch book but wider.
A latter term is a rational manifestation of the former

For m.p. it is necessary next:

• at least 2 interested parties: arbitrageur and agent
• members of one side(agents!) have a strong affinity for SOMETHING that the other side provides them
• the other party(arbitrageur) sees this affinity (as a weakness or necessity) and exploits it at the expanse of the opposite party
• a legitimate process that respects the laws of supply and demand

The end result of this process is that the party motivated by desire is financially exhausted

Model, its manifestation, for above exploitation is called Dutch book!

Economic theory and money pump

In economic theory above conditions are interpreted as the assumption that agents act preferences that satisfy particular requirements of rational consistency
The mechanism which forces the same consistency is called money pump arguments
Economic theorists widely overstep his area with the assumption that these arguments have their foundation only in the agent’s irrational side

Consequences of psychological determination of money pumps arguments

The money pump argument is the justification for the consistency of preferences in economic settings
That essentially means this: Arbitrageurs could exploit people with inconsistent preferences until they forced to leave the market

Irrationality reflects itself in the next term: Intransitiviti
Intransitiviti is, according to them, a factor by which an arbitrageur
would be able to extract money from an inconsistent agent
indefinitely, without providing any services in return, by presenting him or
her with a carefully chosen sequence of trades!

To this be true, agents behave as if they had consistent preferences in the foundations of which stands the inconsistency caused by intransitivity

Again, due to these arguments, an arbitrageur would be able to extract money from an INCONSISTENT agent indefinitely!!

So blind betting which makes up more than 97% of such market failures may be happening because of bettor inconsistency

If we leave these arguments exclusively in the psychological sphere, then something interesting follows when expanding the scope of the meaning of the term money pump

Expanding the enclaves of the term money pump arguments

If we leave these arguments exclusively in the psychological sphere, then something interesting follows when expanding the scope of the meaning of the term m.p arguments

Let’s assume that >Blindness< doesn’t appear only in betting, then it can take on different manifestations-for example in banking
Understanding the matter in this way, we must extend the range of m.p arguments beyond the psychological sphere.
More precisely, if we have to look for both an arbiter and an agent on the rational side
Rationality allows the agent to at least try to turn the direction of the money pump in his own favor so that he too creates his own Duch book

Clash of Dutch books!
This is why this site is for!

Examples of money pump arguments

Taking out of a cash loan

Let’s go back to banking
A money pump appears when the agent(here client) takes out a loan!

Here the agent at the beginning of the process receives a sum of money N while at the end he returns to arbitrageur N + alpha
Arbitrageur in the end has a positive balance, while the agent(client) has a negative balance: -alpha

Everything that contains information about the principal, annuity, and loan repayment duration,…..is a Dutch book, although bankers call it different!

Multiple money pump arguments-The Tree fruits argument

Let us suppose there are three fruits: one apple, one pear, and one banana,
and observe an agent who has preferences about these fruits that are intransitive!

Agents’ preferences:
strictly (intransitively !) prefers:
the pear to the apple
the banana to the pear
the apple to the banana

An arbitrageur first offers to exchange the apple for the pear, then offers the pear for the banana, and finally offers the banana for the apple.

Cubitt, Sugden (2001)
On Money Pumps
In: Games and Economic Behaviour pp. 121-160

Because of his preferences, the agent can be manipulated by an intelligent arbitrator who knows his propensities!

Let’s look now!

Suppose the agent has apples in his possession.
Manipulation begins in a way that the arbitrageur first offers to exchange the apple for the pear, and in return asks for a small fee, δpear
Next offers to exchange the pear for the banana also for a small fee in return, δ_banana
Finally, arbitrageur offers banana for the apple with δ_apple

The agent started with apple and ended up with apple, but with money loss:
δ_pear + δ_banana  + δ_apple  in one cycle

After n cycles  agents end up again with apple but with
n*( δ_pear + δ_banana  + δ_apple  )

money less on his account

Finally, the agent’s (psychological)preferences(manifested through CONSISTENT INTRANSITIVITY) lead him toward his own financial ruin

Game example with 2 money pump arguments

(from Davidson, McKinsey, and Suppes,1955)

In their example, there are two “tickets”, each of which entitles the bearer to play a gambling game once.
Any money paid to obtain the ticket does not count towards the stake for the game. An example of the type of tickets available are:

• Ticket A gives a chance to play a game where you stake 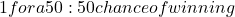5- more desirable
• Ticket B gives a chance to play a game where you stake 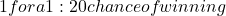100.- more valuable

In these 2 arguments case, B represents intransitive preference, as opposed to A

Money pump process:

The operator offers the customer a chance to buy ticket B at a fairly negotiated price, say P

The operator then offers the customer ticket A in exchange for ticket B, on the grounds that they desire it more

The operator then offers to buy ticket A back for a fairly negotiated price, say P’

Since A is considered less valuable than B, P’ should be less than P.
But after all these transactions, all that has happened is that (P-P’) dollars have been transferred from the agent(punter) to the arbitrageur (in this case operator) in exchange for ultimately nothing

After a sufficiently large number of transactions, n, the final balance is:
for the organizer: n(P-P’)
while for the agent: n(P’-P) which he settles on account of his assets!

The only thing that can happen to him, is eventually he might win 100, and because of his consistent intransitivity, he has lost everything.

Yet, appropriately modified, this idea leads to Betting exchange services, which are the basis for what is called Matched betting

Dutch book

The very idea of how a Dutch book is done was analyzed by Mike Fletcher, Westminster College, Oxford, England, … in his excellent article titled
“Odds that don’t add up!” from 1994

If somebody wants to spend €30  article can be found on this link
or you can continue reading this part of page for free

Creation, the first example

Based on the total sum of paid money(so-called pool) distributed on 4 horses, Fletcher shows the primary method of forming the coefficients-Odds through the following steps:

step 1:forming probabilities

£ I bet on horse A
£ 2 bet on horse B
£ 3 bet on horse C
£ 4 bet on horse D

paid money: 10 £

Probabilities for horse winning:

A…… 1/10
B……. 2/10
C……. 3/10
D……..4/10

Note that the above probabilities are the sole result of a financial calculation

 step 2 : translating probabilities into odds

Probability 1/10=0.1 means that horse A in 10 runs will win 1 time!
So in the other 9 races, A will not win
Now the bookmaker based on this formulate FRACTIONAL ODDS:
9/1 ……. [ (10-1)/1]
Because for horse A odds are 9 against and 1 for

What is the financial interpretation of the FRACTIONAL ODDS?

In this concrete case, 9/1 or 9:1 means that for every invested x pounds if a bet is winning bettor(punter) will earn 9 * x net profit

e.g. for 2 pounds paid in the bet on horse A the possible income will be
9 * 2 = 18 pounds
Revenue will be:92+2=20£ It is useful to notice and remember the following: 9*2+2=2(9+1)=210

Thus we came very close to the cognition that Fractional odds, f.o in the financial plane determine profit, while European odds, d.o, in the same plane determine revenue (stake + profit)

As we determined a connection between f.o and d.o earlier:

d.o=f.o +1

Let’s work out for exercise step 2. in the case of horse C and horse D:

Given from payments:
C……. 3/10 ……..[(10-3)/3]=7/3
In case horse C : 7 against and 3 for -> f.o(C)=7/3
D……..4/10 ……….[(10-4)/4]=6/4=3/2 -> f.o(D)=3/2

Fletcher further states for the bookie’s side:

“If he offers these odds of 9: 1, 4: 1 ,7:3, 6:4 on horses A, B, C, D respectively, then he would be certain to break even”

To make sure of that let’s consider a case when horse D wining

Bookie gives out to people who place bets on horse D(four of them!):
3/24 + 41(stake)=4(3/2 +1)=42.5=10
So, just as much as the total paid: Brake even case!

No matter which horse wins, the bookie will pay 10 pounds

If he(bookie!) wishes to achieve a profit he is forced to create a Dutch book
To do so, he must probabilities that up to 1:
1/d.o(A)+ 1/d.o(B) + 1/d.o(C) +1/d.o(D)

replace with so-called implied probabilities:
1/d.o(A)+ 1/d.o(B) + 1/d.o(C) +1/d.o(D)>1

step 3-implied probability

Transition is provided with  multiplication factor:1/(1-profit_bookie)

Monomial profit_bookie is his wanted profit in percentage, it’s an arbitrary value
If he chooses profit_bookie  =0.2 (20% profit) then we got for:

horse A
1/d.o(A) * 1/0.8 = p(A)*10/8 =1/10 * 10/8=1/8
Value 1/8 is the value of implied probability that horse A wins, p_implied(A)

horse B:

1/d.o(B) * 1/0.8 = p(B)*10/8 =2/10 *10/8 =1/4
Value 1/4 is the value of implied probability that horse B wins, p_implied(B)

horse C:

1/d.o(C) * 1/0.8 = p(C)*10/8=3/10*10/8=3/8
Value 3/8 is the value of implied probability that horse C wins, p_implied(C)

horse D:

1/d.o(D) * 1/0.8 = p(D)*10/8=4/10*10/8=1/2
Value 1/2 is the value of implied probability that horse D wins, p_implied(D)

Finally, we have got:

p_implied(A) + p_implied(B) + p_implied(C) + p_implied(D)=1/8+2/8+3/8+4/8=10/8
p_implied(A) + p_implied(B) + p_implied(C) + p_implied(D)=1.25 > 1=p(A)+ p(B)+ p(C)+p(D)

Does implied probability guarantee an expected profit that doesn’t depend on the winner of the race?

Let’s make sure through the calculation!

Horse A:
implied probability: 1/8
Interpretation- in 8 races horse A will wins onetime and 7 time will lose
f.o(A)=(8-1)/1 = 7/1

Payoff: 7/1*1 +1 =8

Horse B:
implied probability:1/4
interpretation- in 4 races horse will win one time and 4-1=3 times will lose
f.o(B)=3/1

Payof:3/1*2+2=8

Horse C:
implied probability:3/8
interpretation- in 8 races horse C will win three times and 8-3=5 times will lose
f.o(C)=5/3

Payoff:5/33+31=8

Horse D:
implied probability:1/2
interpretation- in 2 races horse D will win one time and 2-1=1 time will lose
f.o(D)=1/1 (evens)

Payof:1/1*4 + 4=8

The purpose of the Dutch book

When a bookie creates a book(Dutch book) he gets profit regardless of the outcome of the event
He does so by increasing the probability
Or what is the same – lowers the height of the odds

Converse Dutch Book Theorem: 

If a set of betting prices obey the probability calculus, then there does not exist a Dutch Book consisting of bets at those prices. 

 The theorem was proved independently by Kemeny (1955) and Lehman (1955)

Duch book, the second example

From example 1 we have the next array of decimal odds(from max to min):
d.o: 8, 4, 8/3, 2
horse A B C D
with the associated, so far unknown stakes:
x_1, x₂, x₃, x₄

But with the condition: x₁ + x₂ + x₃ + x₄=our stake

What we want is to get the same profit regardless of the race winner

In that case, it must be fulfilled:

8*x₁=2*x₄  so  x₁ =1/4 * x₄

by the same logic:

4*x₂=2*x₄  so  x₂ =1/2 * x₄

and

8/3*x₃=2*x₄  so  x₂ =6/8 * x₄

Based on the previous, we get:

1/4 * x₄ + 1/2 * x₄ + 6/8 * x₄ + x₄  =400

(1/4 + 1/2 + 3/4 + 1) x₄ =400

 [1/4 + 2/4 + ¾ +4/4] x₄ =400

5/2 * x4 =400 => x4=160
x1=1/4 * 160=40
x2=1/2*160=80
x3=6/8*160=120

We know we get the same revenue no matter which horse wins
If e.g. horse:
A wins our revenue is: 840=320 quids
C wins revenue is 8/3120=320 quids

No matter the outcome, the bookie’s profit stays at 20% of paid money:400 quids

Dutch book or lock is a set of odds in bets which guarantees a profit, regardless of the outcome of the gamble
if a set of betting prices violate the probability calculus, then there is a Dutch Book consisting of bets at those prices: Dutch Book Theorem

Some historical sketches related to the Dutch book

Lehman (1955) writes:
If a bettor is quite foolish in his choice of the rates at which he will bet, an opponent can win money from him no matter what happens… Such a losing book is called by [bookmakers] a “dutch book” (251).

Lehman, R. Sherman, ‘On Confirmation and Rational Betting’,
The Journal of Symbolic Logic, Vol. 20, No. 3, (1955), September, 251-­62

Ramsey’s ground­breaking paper ‘Truth and Probability (1926), which inaugurates 

the Dutch Book argument, speaks of ‘ a book being made against you ’

‘Having degrees of belief obeying the laws of probability implies a further measure of consistency, namely such a consistency between the odds acceptable on different propositions as shall prevent a book being made against you.’

Ramsey, ‘Truth and  Probability (1926).

Conclusion

The punter has 2 powerful enemies:

• Processes that are exclusively described by random variables
• Dutch book

if subjective probabilities do not satisfy probability axioms, the second enemy is born: a “Dutch Book”—a collection of bets which would ensure sure losses for the holder of these “incoherent” beliefs, regardless of the outcome of the random events.