Expected value in bet-general determinants
a) definition(Wiki); The Expected Value in bet shows how much ones can expect to win (on average) per bet
b) Further notion: It’s the most valuable calculation a punter can make when comparing bookmaker’s odds
c) and finally, a formula:
EV=(Probability of Winning) x (Amount Won per Bet) – (Probability of Losing) x (Amount Lost per Bet)
Nobody could find any fallacy in the above description, but there are a lot of cavities to fulfill
But first thing first:
Random variable
example 1:rolling a dice
The cube has 6 sides and on each side a is placed certain number of dots-from 1 to 6
To describe exactly all the outcomes of rolling the dice, a random variable X is introduced
X= ![]()
The probability of occurrence of any number of points on dice is always the same and amounts to 1/6
This is of course true for an ideal cube
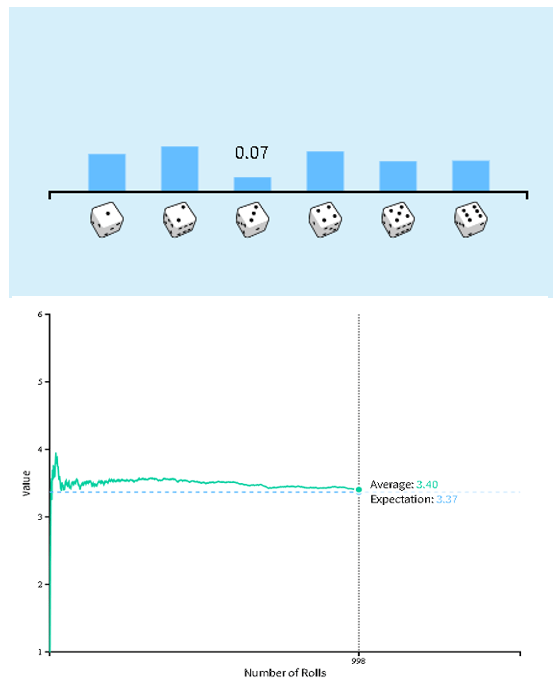
So let’s look at one ‘fixed’ cube
X= ![]()
The picture visually shows the distribution of probabilities by the number of points and avg and e.v for that ‘fixed’ random variable X:
In order to use the random variable X as a betting tool, we have to transform it into a more suitable form!
Let’s say we want to bet on *** (of course we don’t know that the dice is ‘fixed’
For this purpose, we put p=0.07 (because we know that the cube is ‘fixed’) and q=1-p =1-0.07=0.93
and thus we create a new random variable Y:
Transformation of a random variable into a suitable form for calculating the expected value for a bet
Y=![]()
the stake must have a negative sign because it ‘leaves’ us, while the profit must have a positive sign, it ‘comes’ toward us
The random variable Y is, as far as the theory is concerned, correctly set, but as far as its practical use is concerned, it needs to be tweaked a little more!
How is profit expressed?
Of course through stake and fractional odds!
We now have a practical form of E.V for betting:
Y=![]()
E.V(Y)=0.07*f.o*stake – stake*0.93
If we want to make a profit from gambling, the expected value of the aimed event must always be greater than zero, so:
f.o>93/7~13.3
If the bookies give decimal odds=10, at first glance it seems like a great opportunity
Let’s assume that we invest €3.5 per roll
How much do we gain or lose on average per rolling?
E.V(Y)=[0.07*9-0.93]*3.5€
E.V(Y)=-1.05 €
So, with a stake of €3.5, we will lose an average of €1.05
Despite the apparently large d.o., we are playing against ourselves!
example 2:rolette
Rolette has 38 spaces enumerated from 1 to 36 + 2 green
The player bets €1 on a single number.
If that number is spun on the wheel, then win €35 + 1€.
Otherwise, he loses his €1
Now can be formulated this question:
How much money should a player expect to win or lose if they play this game repeatedly?
First, we need to create a random variable Y, related to the considered Bernoulli process!
Y=![]()
EV(Y)=35/38-37/38=-2/38=-0.053€
In other words, on average player lose 5.3 cents per space he bet on.
Indeed if he fulfills all 38 spaces he will certainly ‘win’ 35€ but also pay 38€ for such a no-losing strategy
example 3:State Lottery
39 balls numbered 1 through 39 are placed in a machine and six of them are drawn at random
If the six numbers drawn match the numbers that a player had chosen, the player wins €1,000,000
If they match:
5 numbers, then win €1000
4 numbers, then win €50
It costs €1 to buy a ticket.
Expected value for any win?
Random variable Y for above question must have next form:
Y=![]()
E.V(Y)=1000000p(6) + 1000p(5) + 50p(4) + -1(1- p(6)+p(5)+p(4))
= 50[2000p(6) + 20*p(5) + p(4)] + p(6)+p(5)+p(4)-1
It remains to calculate the required probabilities!
and that I’ll leave the reader to accomplish that task