Dutching stakes allocation – a formula

A heuristic example for Dutching stakes allocation

Dutching stakes allocation is tightly in operationally level connected with the process of Dutching
We know that in a Dutching must be fulfilled next:
s₀+s₁+s₂=S              dividing stake, here in 3 minor ones      I
n_rev=d₁*s₁=d₀s₀=d₂s₂  possible revenue doesn’t depend on outcome   II
But where in here coming Dutching stakes allocation?

If we put II. in I. it follows:
n_rev=S/(1/d₀ +1/d₁+1/d₂)        …………………III

Written differently:
n_rev=S/(p₀ +p₁+p₂)  

  From the above formula, we actually see why Dutching can bring a profit!
p₁ +p₀+p₂   must be less than unity:
      p₁ +p₀+p₂  <1
Otherwise, we deal with Dutch book!

For that case, and only for that case is:   S/(p₁ +p₀+p₂)  > S
From the bookmaker’s point of view, p1 +p0+p2  >1 is conditio sine qua non, a condition without which he, the bookie, would experience guaranteed bankruptcy!

In that case:

S/(p₁ +p₀+p₂)  = n_rev < S
As we now know, tend to profit in that for punter bad option is called Arb(itrary) betting
The above formula(III.) allows to(again) introduce of so-called compound odds, c.o:
n_rev=S*c.o(d.o(0),d.o(1),d.o(2)
where is:
c.o(d.0(1),d.o(0),d.o(2)= 1/(1/d.o(0) +1/d.o(1)+1/d.o(2))

or more practical (in excel) :
c.o=1/3*H(d.o(0),d.o(1),d.o(2)  
where H is the harmonic mean

Function c.o, compound odds, allows us to directly determine the revenue from the initial, undivided stake, S !

Concrete example

 We have the following offer:

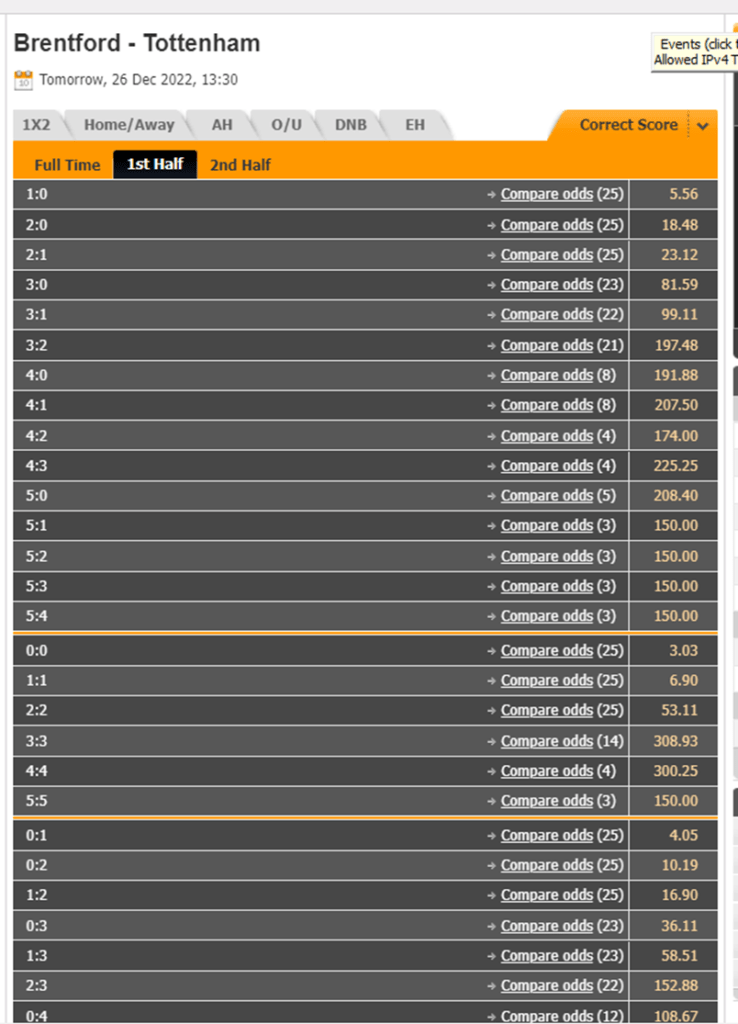
From an indeed rich offer, let’s choose 3 of them as possible result in 1-st half:
0-0 ->d.o=3.03
1-0 -> d.o=5.56
0-1 -> d.o=4.05

What is the high possible revenue for that choice, n_rev ?
The answer to the previous question gives us compound odds, c.o,  as a function of decimal odds by our choice:
c.o(3.03,5.56,4.05)=1/3 * H(3.03,5.56, 4.05)

On excel:

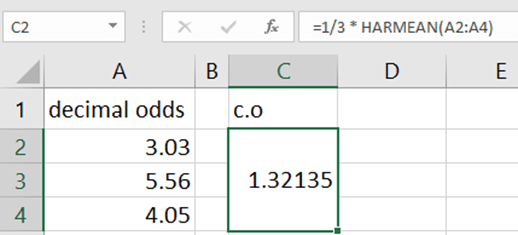
n_rev=S*c.o(3.03,5.56,4.05)=1/3 * H(3.03,5.56, 4.05)
where, as we know, S represents a total stake!

In case the outcome of the first half “falls” within our choice, our profit will be  32.135% of the total stake S

(and it did!
Brentford win 1-half with 1-0)

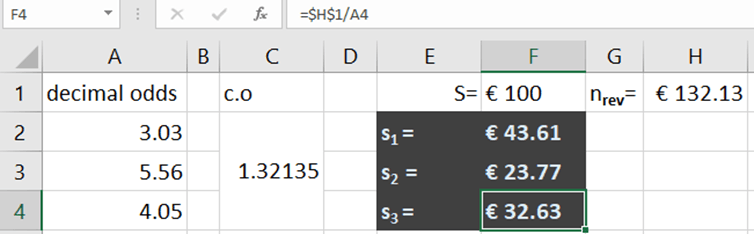
If the bet was S= €100, the problem of allocation of individual stakes still remains!
Because possible revenue doesn’t depend on the outcome, what is written like this: 
n_rev=d₁*s₁=d₀*s₀=d₂*s₂  

The first allocation of total stake S is:
s₁=n_rev/d.o(1)
This can equally be written as:
s₁=n_rev*p(1)= p(1)/(p(1)+p(2)+p(3)

In excel,  the whole allocation model looks like this:

Wider case of allocation

Suppose we want to cover up more possibilities!
The procedure is the same but with slightly altered formulas for compound odds!

A complete offer of odds for the considered event:

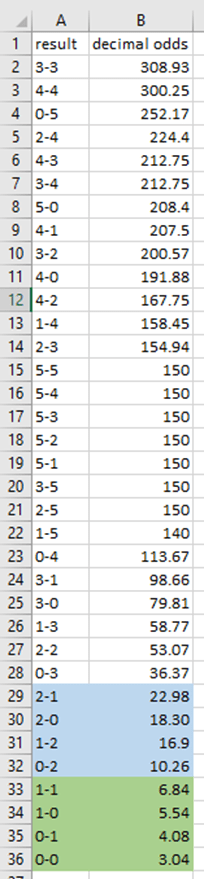
Sum of probabilities for all 35 outcomes is p_bookie=1.367106 , so overround is  very high, >36%
It isn’t a fair offer!!

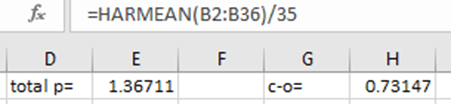
So if we cover up all 35 results we will win, of cause but lose 1-0.7314=26.85% of the total stake, S

If we choose the ‘green area’, the lowest 4 coefficients, c.o= 1.110186 so our initial stake will be increased by 11%
the formula for c.o in Excel:

c.o==HARMEAN(B33:B36)/4

Let’s now dive into the pure mathematical analysis of the allocation in Dutching and build the solid foundations on which the above examples are explained

Dutching Formula and Dutching stakes allocation-derivation

Let’s first recall the (almost)necessary terms!

• allocation, α:   coefficient for determent amount  of particular stake in multiple lays
• dimension, δ: number of partial stakes
• combined odd, c.o : H(x₁.x₂,…x_δ) /δ  where:
  • x_i-particular   decimal odd
  • H-harmonic mean
• Potential,S: Total investment
• p_i=1/x_i : implied probability

Recall the definition of Dutching:

Adjusting multiple stakes in a manner that you win equal net income if either your selection win”

Let’s do the math1.

1. Flegenheimer- Bergman’s condition: “Adjusting multiple stakes…”
α₁*S + α₂*S +…. +α_δ *S =S      => α₁ + α₂ +…. +α_δ =1
From here we got this: ∀i 0<α_i < 1 i=1,2,3…δ

2. Flegenheimer- Bergman’s condition:
”…. win equal net income if either your selection win”
So, ∀i,j α_i *S*x_i = α_j * S * x_j
Suppose that j=δ is the largest index!

From 2.fbc we get as follows:

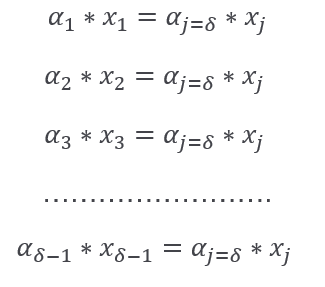
By summing this ‘delta minus one’ equation it follows:

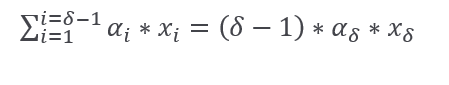
The natural assumption is this:

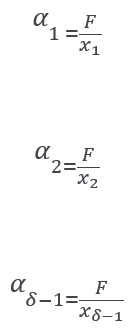
F in for now unknown term/function!

If the above is valid for i=1,2,3….δ-1 then from 2.fbc we got:

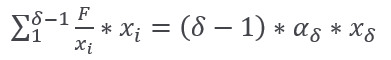
(δ-1)*F=( δ-1)*α_δ*x_δ

So our assumption (by the principle of the mathematical induction
( 5._th Peano’s Axiom)!) has been correct for any dimension δ !

Form of unknown term F we can rich from 1.fbc:

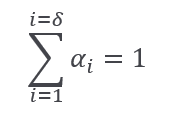
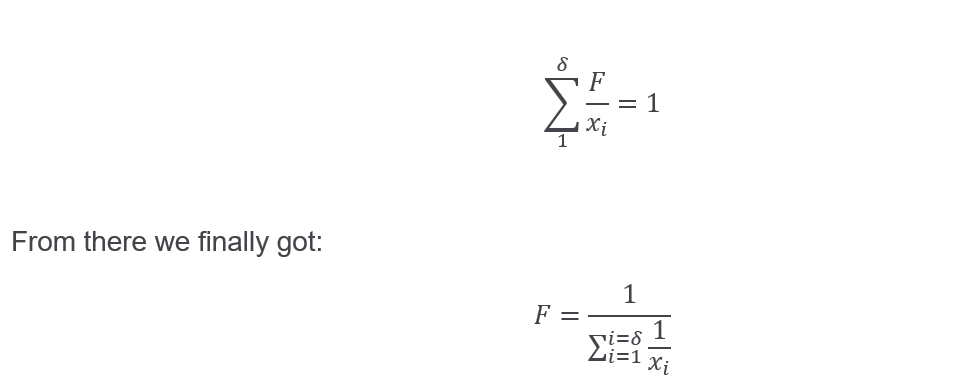
 We know that x₁,x₂….  are odds-so 1/x_i  is  (from odd!) implied probability

Thus we have:

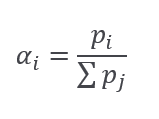
And we got a formula of the same form earlier, for a heuristic example from the introduction of this post!

Let’s go one step further by introducing Allocation Set, A_S, set of all function that satisfies 1.fbc

The theorem about the cardinality of the Allocation set

Allocation Set is not finite e.g card[A_S] >k , ∀k ∊ N

Proof:

Let t be any element from N( so, natural number)

and take into consideration the following:

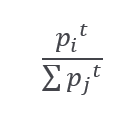
If we sum up the above ratio from i=1 to i= δ we got:

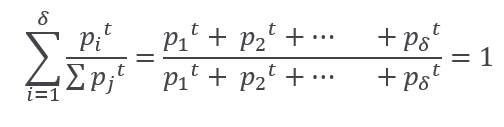
So, we found that:

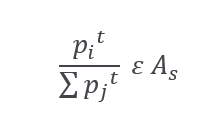
For purpose of continuing the proof of the above theorem, let’s introduce the second main form of allocation:

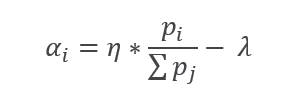
Putting the above expression in 1.fbc we got:

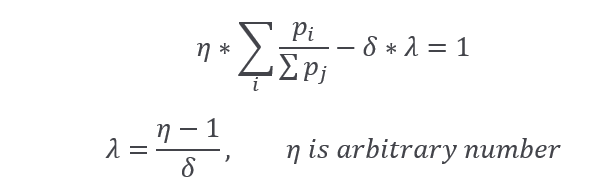
Following that path, we finally have:

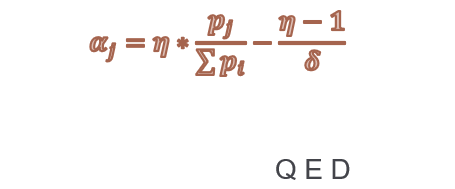
Proof of the above theorem enables follow formulation of the Natural allocation set,NA(η,k) as a set of all αj with the following notation:

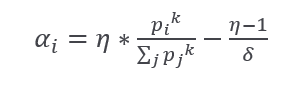
T(Basic theorem about Dutching):

a)   only elements from N_A(η,k) satisfies condition ∑_δα_j =1 , j=1,2…δ
b) only elements from N_A(1,1) satisfies 2f.b condition

Proof:

a)

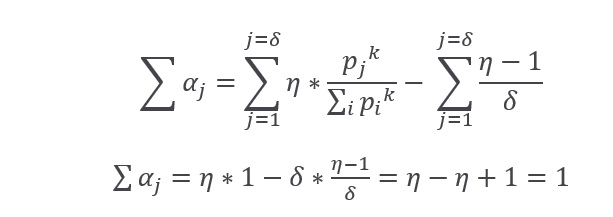
b)

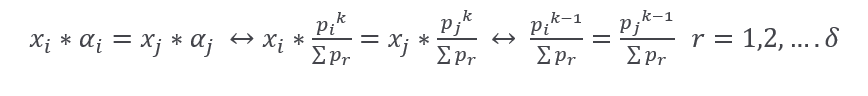
Q.E.D