An important corollary of the Dutching stake allocation theorem can be formulated like this:
In Dutching exist a positive number greater than zero by which we can correctly estimate the possible gain of invested money called compound odds:
c.o : H(x1.x2,…xδ)/ δ
where δ is the number of dimensions in which we operate
Proof:
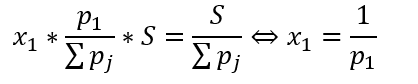
Because d.o is really the inverse of implied probability, left equality is valid!
We can continue with left δ-1 equalities:
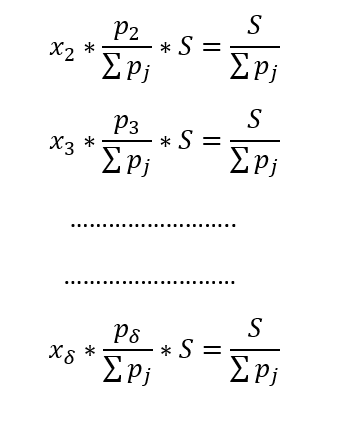
If we sum up these δ equalities :
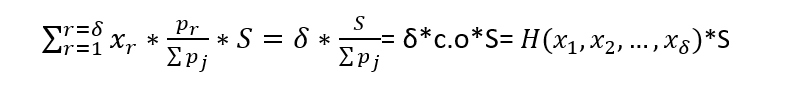
Actually, we proved the next interesting thing:
There is a unique number named compounded odds which pointing what exact amount of net profit we can earn if we adjust stakes in a manner described as Dutching
Or, below the hyperplane which with the coordinate axes of the delta dimensional coordinate system forms a delta dimensional tetrahedron within exists an area within which there is an increased possibility of obtaining revenue
The measure of that potential revenue, a unique number, called compound odds can be calculated by the formula:
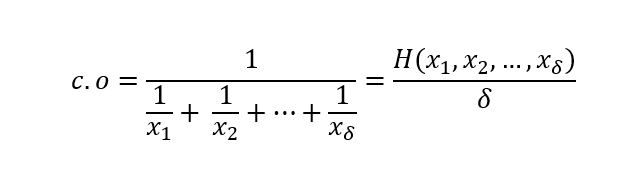
Let’s take a closer look at the expression c.o*S
It is similar to d.o*S in case of single selection, or accumulation
d.o*S contains stake plus eventual net profit, so d.o*S= S+ ρ*S because it is generally valid:d.o=1+f.o
The resulting expression, c.o*S has the same meaning.
It may or may not contain net profit because among other conditions it deeply depends on over-round (c.o<1)or under-round(c.o >1)
Discussing Σpr (very important)
Σpr =p1 + p2 +…… + pδ
As we know, dealing with bookie offers, 1- Σpr < 0 and Σpr -1>0 is called overround, vigoris, juice, etc
So if we stick with one bookie always must be r < number of all given markets
For example, if we bet on 1. half/2.half in a football game, the market has this structure:
{1,0,2}X(1,0,2}=[(1,1),(1,0),(1,2),(0,1),(0,0),(0,2),(2,1),(2,0),(2,2)}
We deal with 9 possibilities
There is not the slightest chance that the sum of all probabilities in the offer of coefficients will be less than 1
Therefore, it must be taken: r<9
From set {1,0,2}X(1,0,2} we could chose its subset: {1,0),(1,2),(0,1),(0,0),(0,2)}
And of course, first {1,0,2) could be the market for a team1 result in 1half of game, and the second {1,0,2] for team2 in 2. half some other game!!
In this particular case, we deal with accumulation!
In that particular case r=5 , and that is our decision and we are faced with the risk of possibly losing our bet!
“Every betting decision you make has to be judged on its own individual merits and dutching doesn’t change that”
Nigel Channing
The easiest way to get to c.o> 1 is to choose a market, combine it from an offer of different bookies
But then, we entering in the area of arbitrary betting if want to cover all possibilities/outcomes