Betting efficacy analysis

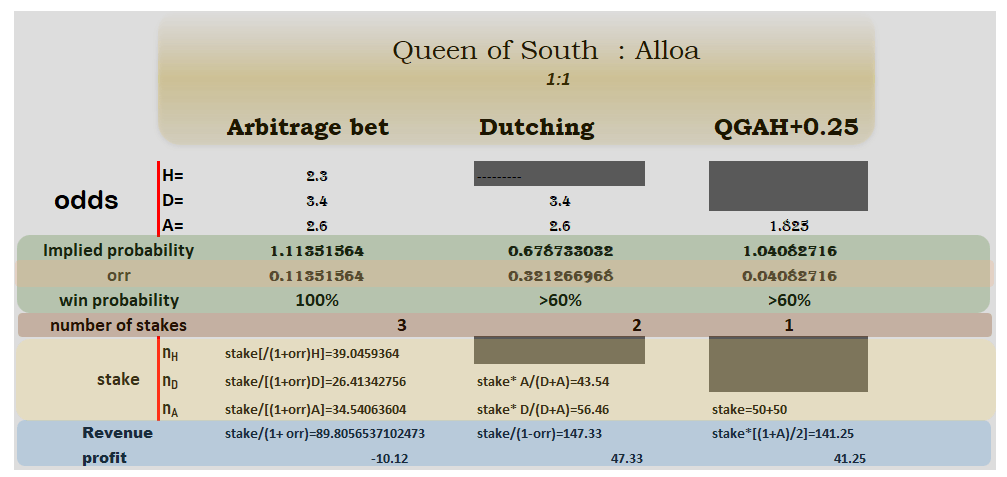
The betting efficacy and after all, the profitability of the mentioned methods will be determined based on these data

For the sake of brevity and clarity, I introduce a more convenient notation:
for :
d.o(H), odds for a home win, briefly: H
d.o(D), odds for a draw result, briefly: D
d.o(A), odds for an Away win, briefly: A

In the concrete analysis we have the next odds:
H=2.3
D=3.4
A=2.6

First Method: Arbitrage betting

Say that we put €100 of stake on Queen of South-Alloa, a game that took place yesterday, October the first, 2022, at 4 pm, Palmerston Park, ended up with outcome-1:1

Is it even profitable?

This question is answered by the harmonic mean:

H(2,3,3,6,3.6)=2.69417 <3
so arbitrage betting is pointless

Ok, there must be a bookie’s overround, orr?

What is its value?

1/H + 1/D + 1/A=1.113516

So the value of overround is 11,35%

What is the percentage of his guaranteed profit, based on orr?

As we know from earlier, the answer to that question is:
profit=orr/(1+orr)*Stake [%]

profit=0.1019=10.19%

There remains the question of allocations-individual payments to 1,0,2 outcomes

Let ∑ denote sum: HD+HA+DH=22.64 (for this given odds)

the first allocation:

n₁(orr)=stake/[(1+orr)H]=€39.04594 stake for home win

the second allocation

n₀(orr)=stake/[(1+orr)D]=€26.41343

the third allocation

n₂(orr)=stake/[(1+orr)A]=€34.54064

From the above formulas come next:

n₁H=n₀D=n₂A=stake/(1+orr)=100/1.113516=€89.80565

And that is the value of revenue from Arbs for this game and bookmaker!

Dutching

Because of the choice of the handicap, we take odds D and A into consideration

If we approach this method from total stake as the starting point then we have to find compound odds,c.o

We find it using the harmonic mean:
c.o(D,A)=H(D,A)/2

c.o=1.473333

So revenue from applying Dutching is:
€100*c.o=€147.333

QGAH+ 0.25 handicap

Because of that handicap, the initial stake must be split into 2 equal parts: each €50

The first part goes for 0.0 handicap and the second for 0.5 handicap

As previous we denote:

d.o(H)=H, d.o(D)=D, d.o(A)=A
in this case
H=2.025 @ -0.25
D=nothing
A=1.825 @ +0.25

first handicap: 0 or draw no bet, betting efficacy

Result of the game: 1-1 therefore DRAW
revenue_NDH=return of stake:€50

second handicap: half-goal handicap, betting efficacy

After offset, the virtual result is 1:1.5 in the advantage of Alloa
so, revenue_{0.5 handicap}=€50*1.825=€91.25

revenue_total=revenue_NDH + revenue_{0.5 handicap}=€141.25

For this values of revenue_NDH and revenue_{0.5 handicap} as we can see Dutching is profitable than QGAH+0.25

Infographic presentation of shown methods