Odds

Some definitions

• Game: an experiment that generates aleatory events
• ODDS: the ratio of payoff to stake, represented by the ratio between the amounts staked by parties to a wager or bet.
• Market: offer from bookies related to events with offered coefficients: simple betting, events associated with Handicap, events related to scored goals, etc.

Because of the aleatory nature of games, those three terms  logically go to each other

What is Bet?

According to John Piper, in his  “Binary Betting-An introductory guide to making money with binary bets” :

“A bet is when money is put at risk in the hope of receiving more cash if a particular event occurs.”
What may happen?
If the bet is won, we get that additional money; if we lose, we usually lose all of the money put at risk.”

What may happen?
“If the bet is won, we get that additional money; if we lose, we usually lose all of the money put at risk.”

Differentiation of Odds by functionality

Depending on which side you look at, mathematical or financial, the odds can be divided into 3 main types:

• European or decimal odds hereinafter referred to as d.o e.g d.o(H)=1.75
• UK or fractional odds which we write as f.o e,g f.o(H)=3/4
• American or Moneyline, favored and tailored by American bookmakers.
  The figure quoted is either positive(underdog) or negative(favorite)

Anyhow it is extremely important to understand the differences between EU and UK type or Moneyline

Decimal odds and implied probability

There is a special connection between d.o(and of carouse f.o) and implied probability expressed through third fundamental formula:

d.o=1/implied_probability

Why is so?
Let’s take as an example an event with p=50%
Probability implies that a favorable outcome will be repeated every other time
Considering that, it is logical that the reward for success should be 2x invested

Let p=25%
this means that a positive outcome (on average) will appear every 4 times
it is natural that d.o=4

Let the ‘real’ probability be p=50%
If the bookie instead offers p1=55%, he, therefore, raises the probability of that outcome, which is obtained with d.O
In the first case d.o=2, while in the second d.o1=1.8181..
So, he lowers the value of the odds by implied probability

Let’s have look at a single bet take from William Hill’s offer:

For home win, bookies offerd d.o(Werder B.)=2.20
The inverse value of a given one is called-Implied or bookies probability

1/2.2=0.454545….~45% so bookies, here W.H ‘thinks’ that Werder has 45% chance of a home win
1/3.2=0.3125~ 31% Werder has 31% chance of draw
1.3,4=0.2941176..~28%

1/2.2 + 1/3.2 + 1/3.6=1.061163..

Let S be the set of all uncertain events s₁,s₂,..s_n
For the function p:S={s₁,s₂,..s_n}-> R to be a probability, it must satisfy, among other this conditions(axioms):
p(s_k)>0 satisfied!
p(S)=1 not satisfied !!

As how will be elaborated later, the implied probability is a protective mechanism for this one who is laying a bet-bookie!

Fractional odds, f.o

F.O is simple to calculate because they are given in fraction form
The denominator is the amount bet and the numerator is the amount that your wager will yield

The offer typically for England bookies is presented in the form of a fraction
a/b ‘a’ to ‘b’ against if a>b or worse than evens
1-1 evens odds if b=a
a/b ‘b’ to ‘a’ on if b>a better than evens

One, financial explanation of  fraction a/b: one should invest b-stake to accomplish a-profit

Let’s have a deeper insight
a)against case
4/2
meaning: for invested every 2 of profit, revenue: 4+2=6 we got 2

Note: same revenue has different profits

Involving f.o with probability

Rolling 1 dice has 6 possible outcomes
Suppose we bet on 5 dots land up
This event has only 1 outcome in our favor, and 5 against, so f.o({5})=5/1
Suppose we bet on 5 or 3 dots land up in one roll
Now 2 outcome goes in our favour and 4 against, f.o({3},{5})=4/2=2/1
Suppose we bet on 5 or even number dots land up in one roll
bet now has 4 outcomes go in our favor and 2 against, f.o=2/4=1/2

Let’s calculate the corresponding probabilities in all 3 cases

1. f.o=5/1
   prob=1/6 => d.o=1/prob….. d.o=6
2. f.o=2/1
   prob=2/6 => d.o=6/2=3
3. f.o=1/2
   prob=4/6 d.o=3/2 = 1.5

In the betting world, we are dealing with so-called bookie’s probability, p_bookie ,- ‘probability’ under influence of Dutch book
Relation between d.o and p_bookie :
d.o= 1/ p_bookie

The connection between bookie probability and fractional odds

Let’s find a general rule for the connection between (game) odds in the form a/b or a-b  and probability in general

It is natural to start from the general form for f.o=a/b
aleatory event (in-game) with fractional odds a/b shows us that game has a+b outcomes
from the mass of a+b outcomes b goes in our favor so corresponded probability is:b/(a+b)

So from the given f.o, the probability we read like this:
from the mass of a+b outcomes b go in our favor so corresponding probability is:b/(a+b)
(f.o=a/b)_prob =  b/(a+b)
shorter: (f.o)_prob = b/(a+b)

Decimal odds of an outcome are equivalent to the decimal value of the fractional odds plus one
Here’s why:

                         1/(f.o)_prob =(a+b)/b= a/b +1  = f.o +1  = d.o

Suppose one invests 8 € in a bet where D.O is 2
In a win situation, one’s income is:
8 D.O= 82€=16€
Therefore those 16 euros are included profit + stake= 8+8
That means for 8€ we got 8€ so in F.O term we got a deal with even odds: 1-1

Rule: The decimal odds of an outcome are equivalent to the decimal value of the fractional odds plus one

Basic mathematical relations

First and main formula(tion):

Revenue=decimal_odds*stake
or expressed by a formula:
R=d.o*s

Second, also main formula(tion):

Profit=fractional odds* stake
or
P=f.o*s

     The above formulations are equally appliable in a single bet or parlay

The difference between d.o and f.o in mathematical terms is due to the difference in meanings of Revenue and Profit in financial terms

Profit is pure cash, income while revenue must include someone’s investment:
Revenue=Profit + invested money

Since Profit is included in Revenue, this fundamental relationship follows:
                                  d.o=f.o + 1

It’s time for a tiny recapitulation!
At the end of the Home page content, we concluded about the nature of the wagering system, while on the About page we have done the same about the mathematical structure previous mentioned nature

With the above formula which connects d.o and f.o possibility of branching out practical methods is open

Let’s prove that even odds 1-1 are quoted in decimal odds as 2.00
1-1 (one to one) 1 profit
Total return:1+1=2
On the other hand, we know that Total return is equal: stake*D.O
Here we got: stake=1$
So from here follows what is claimed

Apostasy coefficient

The ratio of profit and revenue is equal according to the latter:
P/R=f.o/d.o=(d.o-1)/d.o=1-1/d.o=1-probability_bookie

Profit/Revenue=q_A

Short explanation: Let’s say that someone intends to bet on an event that will happen on 13. August 2022

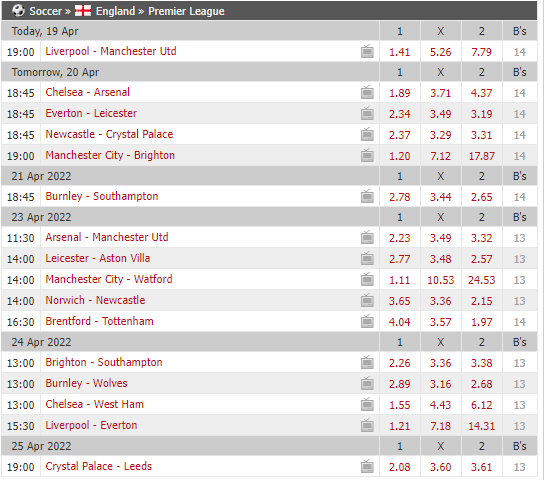
	1	0	2
Arsenal Leicester	1.61	4.20	5.49

d.o(H)=1.61 which Implies, according to the bookie’s estimation, that Arsenal has 1/1.61=0.6211180124… ˇ62% chance to win Leicester

If we take that ‘probability’ as a referent point, the probability of Arsenal not winning is 1-0.6211180124…=37.88%
and that value: 37.88% is q_A or apostasy coefficient

So, whatever could be high or low possible revenue, the ratio between profit and revenue would be constant, exactly:q_A !
If we denote a total mass of revenue as 1 then we get the following:

Profit=q_A

So if Arsenal wins then the profit of that success bet will be equal to the probability of Arsenal not winning