Geometric interpretation of Dutch book
In football events, as we already know, there are 3 possible outcomes:
Home win(1), Draw(0), Away(2) win
significant for the Spatial view of the Dutch book
Important: if the sum probabilities of all outcomes add up to 1 then we deal with so-called true odds!
P(H)+P(D)+ P(A)=1
The Main equation
This equation is of great importance
It can be considered as one pillar for a rational approach to betting.
Therefore, it will be hereinafter referred to as the Main equation
Along with this equality, the following two more come in importance:
P(H)+P(D)+ P(A)> 1 upper
and
P(H)+P(D)+ P(A)<1 lower
are main Inequations (upper and lower)
The upper main inequation belongs to a bookie and contains all Dutch book polyhedrons
Lower grand inequation, on the contrary, belongs to punters and contains all Arb polyhedrons
Spatial geometry of Main equation
If we P(H) substitute with x, P(D) with y, and P(A) with z then we get next:
x + y + z=1
And that is nothing but the equation of one specific plane in 3D space!
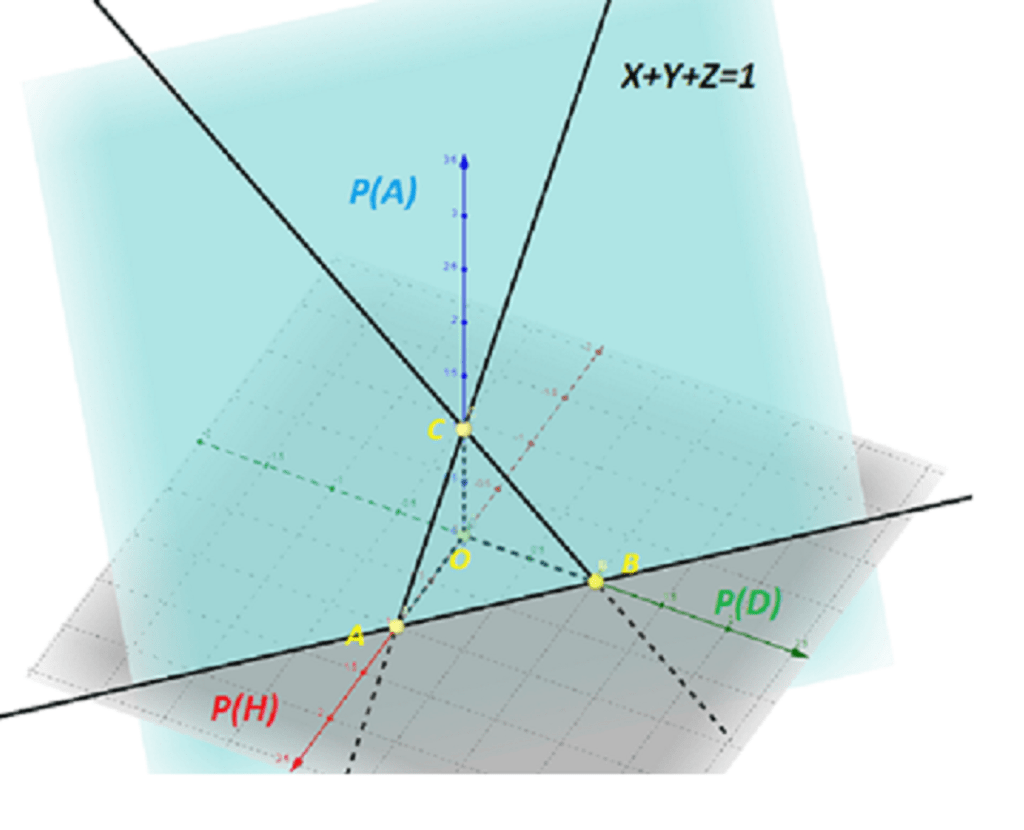
In 3D, the equation of the XY plane (in gray) is Z = 0
In the same way, the equation of the XZ plane is Y = 0
Obviously, the equation of the YZ plane in the same 3D space must be: X = 0
The plane x + y + z = 1 intersects the plane Z = 0 in the (infinite) line which passing through points A and B
Similarly, the same plane intersects the plane Y = 0 in line passing points A and C
Plain X=0 intersects plain x+y+z=1 in line to which points B and C belong
These sections form an interesting geometric body with 4 facets and 6 edges called-Tetrahedron
The main facet of the Dutch book tetrahedron
Facet ABC is of primary bookie’s interest because by ‘extending’ its geometry he makes a profit!
In what way does he ‘extend’ that geometry?
By “hyperbolically” increasing the values of the associated probabilities!
This type of increase results in a decrease in the value of the coefficients
Let’s repeat:
In the process of placing a bet, the bookie stands on one,laying side, while the punter is on the opposite –backing side
This is the basic difference between them – the one-by position within the betting process
The main facet is, we can say that is a place where these two different processes meet each other!
This difference in positions goes in the bookie’s favor because it allows him to always profit without knowing the complicated mathematical-financial system!
How is that?
Misconceptions related to laying bets of laying a bets
Because he disobeys the law of probability in a manner that sum all probabilities exciding the unity
A consequence of disobeying is next:
xp(H) + xp(D) + xp(A)=x
And as we know: x=1/(1-y) where y is the bookie’s profit in percentage
(these x and y have nothing to do with the x, y in the equation of the plane in 3d!!)
The hyperbolic multiplier can also be given another form: x=1+ orr
where orr is so-called overround
Because x ≠ x-1 so orr isn’t the same as bookie’s profit opportunity
Many sources on the web did glide in deep misconceptions about these two different things
Investopedia, unfortunately, is no exception

Profit opportunity and Overround-differences
1+ orr=1/(1-y)
orr=1/(1-y)-1=(1-1+y)/(1-y)
Overround as a function of bookie’s profit opportunity
orr=y/(1-y)
Bookie’s profit opportunity as a function of overround:
(1-y)orr=y => y+orry=orr
y(orr)=orr/(1+orr)
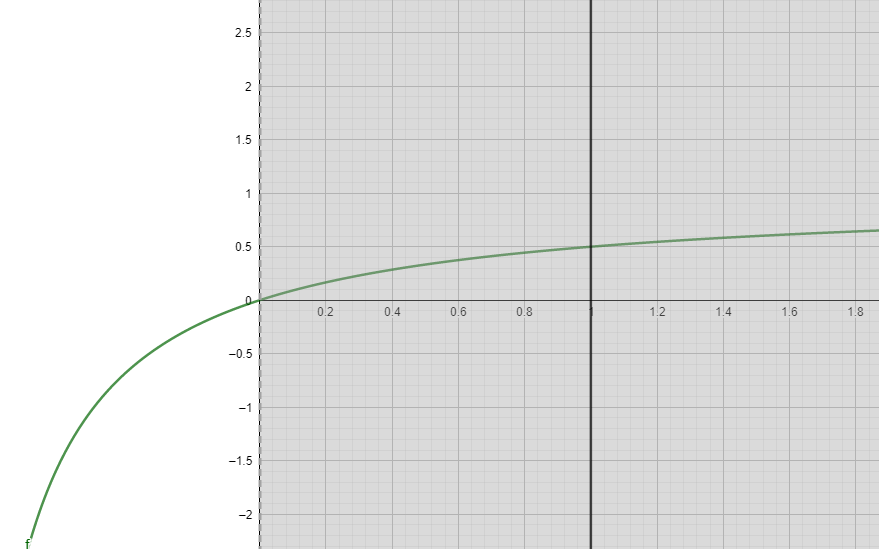
If orr=5% then the bookie’s profit opportunity is exactly:
y=0.05/1.005
y=0.0497512437810946 (on fifteen decimal correct)
Wow!
Looks like Investopedia has right
Hm!
But if we take orr=9% then y=0.09/1.09=0.0825=8.25%
In logic a conditional statement: p→q is false
if and only if the premise p is true and the conclusion q is false.
p→q is logically equivalent to q∨¬p
So if p is false, then ¬p is true and q ∨¬p is also true.
Thus p→q is always true
/in other words from false fact may follow a true conclusion/
One criterion linked with the Dutch book polyhedron
In general, for orr>0 it holds that the bookie’s profit opportunity is lesser than overround
Truly:
1/(1+orr)<1 for every orr>0
If we put 1/(1+orr)=k <1
then follow y=orr*k < orr
Main Theorem of the Dutch book:
Let d.o’(H),d,o’(D), and d.o’(A) be the coefficients, odds, derived by the hyperbolic growth of real probabilities
Conclusion:
Their harmonic mean is always less than 3
i.e
H(d.o’(H),d,o’(D), d.o’(A))<3
proof:
hyperbolic increasing of ‘real’ probabilities implies:
d.o’(H)=(1-y)d.o(H)
d,o’(D) =(1-y)d.o(D)
d.o’(A)= (1-y)d.o(A)
Harmonic mean by definition gives:
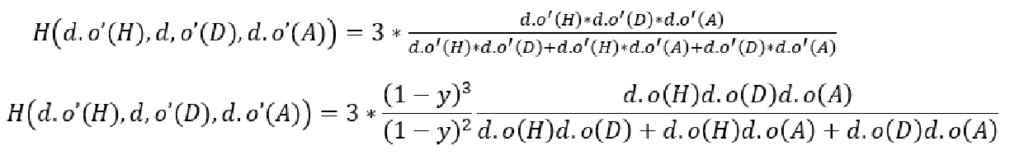
Considering that on facet ABC must be fulfilled:
p(H)+p(D)+p(A)=1 must be also fulfilled:
d.o(H)d.o(D)+d.o(H)d.o(A)+d.o(D)d.o(A) = d.o(H)d.o(D)d.o(A)
from here we got:
H(d.o’(H),d,o’(D),d.o’(A))=3(1-y) & y>0 =>
H(d.o’(H),d,o’(D),d.o’(A))< 3
Q.E.D
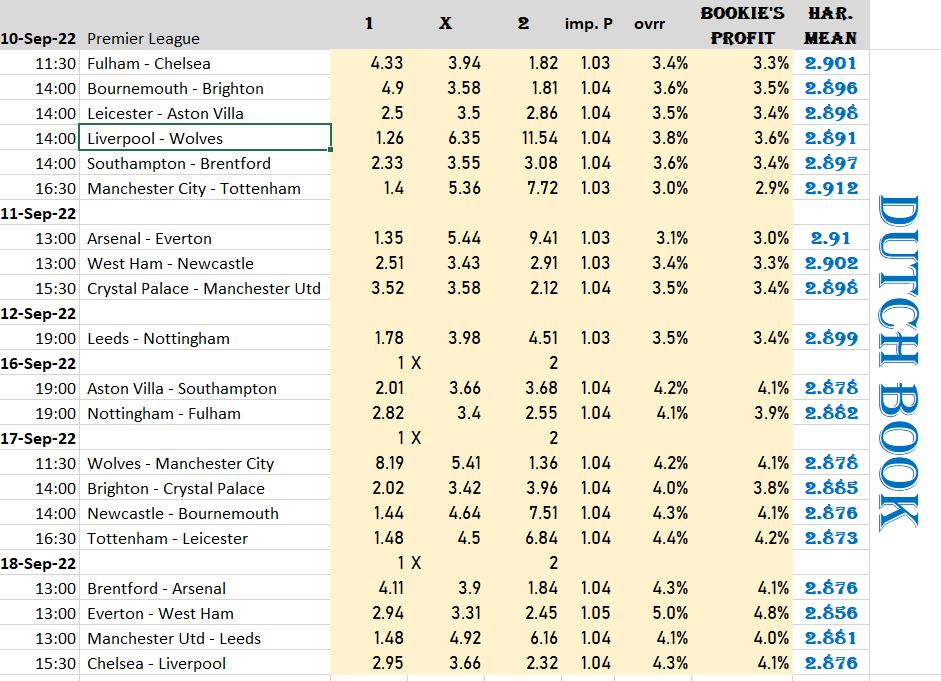
The application of the above theorem is reflected in this table, an overview of the odds for the Premier League for September 2022: