Dutch book in football bet
Let’s continue with the Dutch book in the spirit of Fletcher’s articles to prepare everything necessary for the introduction of the Dutch polyhedron!
Bundesliga- the match between Dortmund and Wolfsburg played on December 17, 2014, with match fair market:
H D A
Dortmund – Wolfsburg 1.75 3.5 6.93
Fairness is reflected through (probabilities that are up to 1):
P(H)+P(D) + P(A)= 1/1.75 + 1/3.5 + 1/6.93 =1
For reality’s sake let’s take that € 50,000 was paid on H, € 25,000 in D, and €12 626 in Wolfsburg’s victory as a guest
So a total of € 87,626 was paid in the bookie’s pool
step 1.- probability estimation
P(H)=50000/87626 =0.5707
P(D)=25000/87626= 0.2853
P(A)=12626/87626= 0.1440
From the bookmaker’s (financial!)point of view, if Dortmund and Wolfsburg would play 87,626 games, first would win 50,000 times and draw 25,000 times…
This perspective was encouraged solely based on bets received!
step 2. translating probability into f.o
f.o(H)=[ 87626-50000,50000]=37626/50000=3/4
f.o(D)=[ 87626-25000,25000]= 62626/25000=5/2
f.o(A)=[ 87626-12626, 12626]=75000/12626 ~ 31/5
Clarifying:
f.o(H)-means that in(according with finance!) 3+4=7 games Dortmund will win 4x and not win 3x
f.o(D)-according to betting pool in 5+2=7 games, Dortmund will draw 2x , not even in 5x
f.o(D)-in 31+5 plays Dortmund wil loose 5x, and not loose 31x
The transition from f.o. to d.o.:
f.o(H)+1=0.75 +1= 1.75252
f.o(D)+1=2.50504+1=3.50504
f.o(A)+1=5.94012+1=6.94012
Probabilities that sum up to unity
“Anyone who violates any law of probability can be suckered via a Dutch book. But if you obey the laws of probability, it’s impossible to be Dutch booked”
Odds & Ends
Introducing Probability & Decision with a Visual Emphasis
Jonathan Weisberg
Suppose that x punters who bet on a draw in a single slip have raised money from betting
How much is left to the bookmaker in such an instance of the market?
Bookmaker received 87626 in bets and pay off to those people who have bet on -draw, an income whose amount is dictated by f.o + initial stake
f.o(D)*25000+ 25000=62626/25000 * 25000 +25000=87626
So, the bookmaker’s leftover is equal to big-nothing!
The absence of Dutch book, among other, provide bookies with 0 profit
Game changer-implementing a Dutch book
Since the bookmakers do not organize betting because of the goodness of their hearts, let’s assume that one of them wants to earn some profit, say a p= 7% of the total payment
To achieve this goal, the bookmaker multiplies the probabilities from phase 1, as we already know by a factor of 1 / (1-p) in that case:1/0.93=1.076
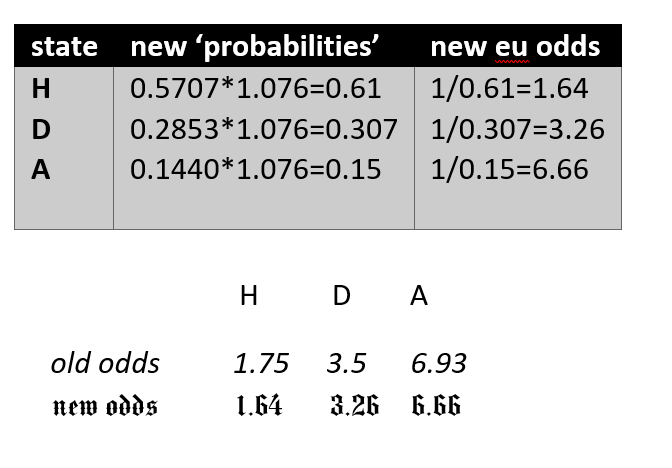
probability which leads to a decreasing odds
Bookmaker received 87626 in bets as in the previous case!
He pays out, to people who have bet on(x of them) -draw, amount dictates by the formula:
(f.o*stake + initial stake)*(1-0.93) =87626*0.93=81 492.18
Therefore, in his cash register stays: 87626-81 492.18=6133.82 or 7% from bet pool
As Fletcher stated :
” The bookmakers’ odds merely reflect the punters’ beliefs. This is an important point because it means that the bookmaker cannot be beaten by the punters.
Any punter who does make a profit is doing so at the expense of other punters.”
Proof of the Dutch book theorem
According to Investopedia, The Dutch Book Theorem is a probability theory that states that profit opportunities will arise when inconsistent probabilities are assumed in a given context.
Suppose we deal with the following 3 states market: H,D,W or what is the same: 1,0,2
Next, let’s assume that it is total payment equal; N=nH +nD + nA
Remark:
The reasoning is also valid for any finite number of market states
Profit equality conditions, p.e.c:
- nH*d.o(H)=N
2. nD*d.o(D)=N
3. nA*d.o(A)=N
After increasing probability we deal with this situation (in the whole market!):
Pbookie=x*P
As is Pbookie >P must be x>0
Supposed form for variable(function!) x:
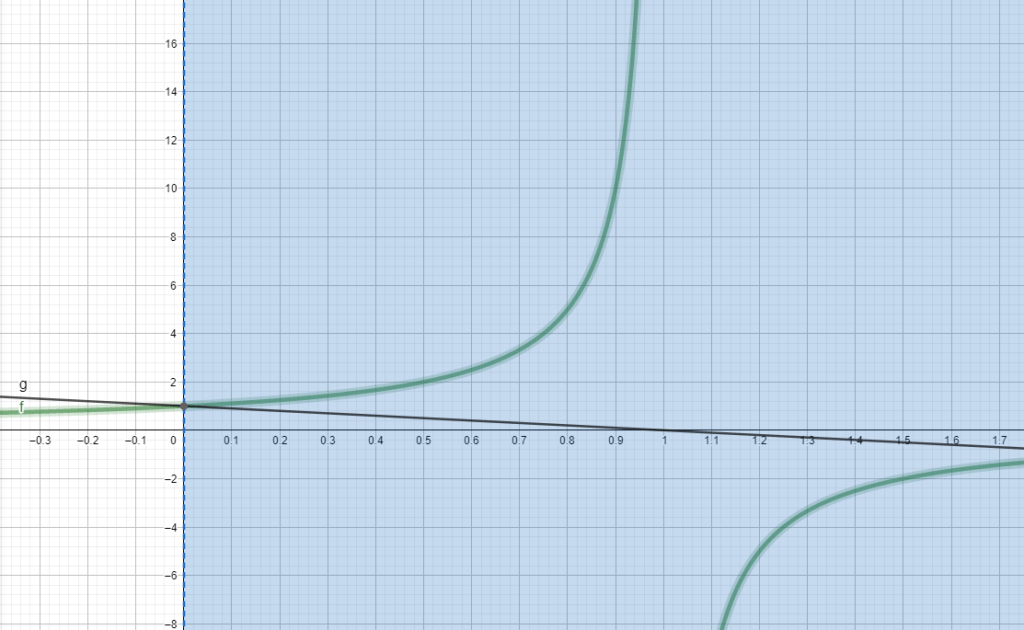
Some explanations.
First off the greenish curve is an equiaxed hyperbola!
More precisely, it is an example of a homographic curve that has this general form: (ay+b)/(cy+d)
In this specific case we have:
a=0, b01, c=-1, d=1
Vertical asymptote: y=- 1/-1=1
horizontal asymptote: x=0
For y=0-> x=1
In this case, there is no Dutch book because d.onew=d.o*1
The black line has the equation z=1-y
When the probability is multiplied by x, then d.o is multiplied by z
For y=0 we have x=1 and z=1
When y increases, then the hyperbola also increases (multiplier for probability), and the line z=1-y (multiplier for d.o) decreases
From above we got:
Pbookie= x*P =1/(1-y) *P => d.obookie =(1-y)d.o
d.obookie =1*d.o -y*d.o
To be strictly mathematically correct, the above equation should be written like this:
d.obookie(s,y))=1*d.o(s) -y*d.o(s)
where the variable s can only take the following values: H,D,A or (finite number market states!)
So only values/states are dictated by the market!
Let’s observe how the function ns behaves as a multiplier:
d.obookie(s,y))*ns= d.o(s)*ns -y*d.o(s)ns
From the p.e.c directly follow:
d.obookie(s,y))*ns =N-y*N , s ε {H,D A}
By increasing the probability for the factor x=1/(1-y), the possible revenue is reduced by the (percentage)factor: y- bookie’s realized profit opportunity